Finding Minimum Simple Spanning Tree With Solutions
We have discussed Kruskal's algorithm for Minimum Spanning Tree. Like Kruskal's algorithm, Prim's algorithm is also a Greedy algorithm. It starts with an empty spanning tree. The idea is to maintain two sets of vertices. The first set contains the vertices already included in the MST, the other set contains the vertices not yet included. At every step, it considers all the edges that connect the two sets, and picks the minimum weight edge from these edges. After picking the edge, it moves the other endpoint of the edge to the set containing MST.
A group of edges that connects two set of vertices in a graph is called cut in graph theory.So, at every step of Prim's algorithm, we find a cut (of two sets, one contains the vertices already included in MST and other contains rest of the vertices), pick the minimum weight edge from the cut and include this vertex to MST Set (the set that contains already included vertices).
How does Prim's Algorithm Work? The idea behind Prim's algorithm is simple, a spanning tree means all vertices must be connected. So the two disjoint subsets (discussed above) of vertices must be connected to make aSpanningTree. And they must be connected with the minimum weight edge to make it aMinimumSpanning Tree.
Become a success story instead of just reading about them. Prepare for coding interviews at Amazon and other top product-based companies with our Amazon Test Series. Includes topic-wise practice questions on all important DSA topics along with 10 practice contests of 2 hours each. Designed by industry experts that will surely help you practice and sharpen your programming skills. Wait no more, start your preparation today!
Algorithm
1) Create a set mstSet that keeps track of vertices already included in MST.
2) Assign a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign key value as 0 for the first vertex so that it is picked first.
3) While mstSet doesn't include all vertices
….a) Pick a vertex u which is not there in mstSet and has minimum key value.
….b) Include u to mstSet.
….c) Update key value of all adjacent vertices of u. To update the key values, iterate through all adjacent vertices. For every adjacent vertex v, if weight of edge u-v is less than the previous key value of v, update the key value as weight of u-v
The idea of using key values is to pick the minimum weight edge from cut. The key values are used only for vertices which are not yet included in MST, the key value for these vertices indicate the minimum weight edges connecting them to the set of vertices included in MST.
Let us understand with the following example:
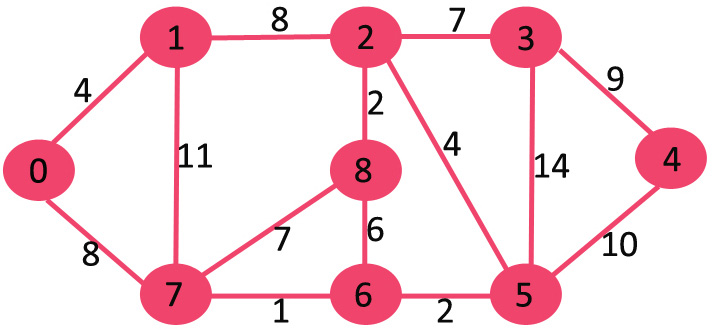
The set mstSet is initially empty and keys assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite. Now pick the vertex with the minimum key value. The vertex 0 is picked, include it in mstSet. So mstSet becomes {0}. After including to mstSet, update key values of adjacent vertices. Adjacent vertices of 0 are 1 and 7. The key values of 1 and 7 are updated as 4 and 8. Following subgraph shows vertices and their key values, only the vertices with finite key values are shown. The vertices included in MST are shown in green color.
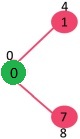
Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8.
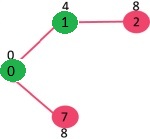
Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (1 and 7 respectively).
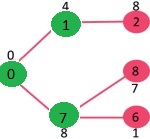
Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated.
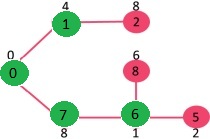
We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.
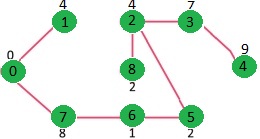
How to implement the above algorithm?
We use a boolean array mstSet[] to represent the set of vertices included in MST. If a value mstSet[v] is true, then vertex v is included in MST, otherwise not. Array key[] is used to store key values of all vertices. Another array parent[] to store indexes of parent nodes in MST. The parent array is the output array which is used to show the constructed MST.
C++
#include <bits/stdc++.h>
using namespace std;
#define V 5
int minKey( int key[], bool mstSet[])
{
int min = INT_MAX, min_index;
for ( int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
void printMST( int parent[], int graph[V][V])
{
cout<< "Edge \tWeight\n" ;
for ( int i = 1; i < V; i++)
cout<<parent[i]<< " - " <<i<< " \t" <<graph[i][parent[i]]<< " \n" ;
}
void primMST( int graph[V][V])
{
int parent[V];
int key[V];
bool mstSet[V];
for ( int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false ;
key[0] = 0;
parent[0] = -1;
for ( int count = 0; count < V - 1; count++)
{
int u = minKey(key, mstSet);
mstSet[u] = true ;
for ( int v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
primMST(graph);
return 0;
}
C
#include <limits.h>
#include <stdbool.h>
#include <stdio.h>
#define V 5
int minKey( int key[], bool mstSet[])
{
int min = INT_MAX, min_index;
for ( int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
int printMST( int parent[], int graph[V][V])
{
printf ( "Edge \tWeight\n" );
for ( int i = 1; i < V; i++)
printf ( "%d - %d \t%d \n" , parent[i], i, graph[i][parent[i]]);
}
void primMST( int graph[V][V])
{
int parent[V];
int key[V];
bool mstSet[V];
for ( int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false ;
key[0] = 0;
parent[0] = -1;
for ( int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true ;
for ( int v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
primMST(graph);
return 0;
}
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class MST {
private static final int V = 5 ;
int minKey( int key[], Boolean mstSet[])
{
int min = Integer.MAX_VALUE, min_index = - 1 ;
for ( int v = 0 ; v < V; v++)
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
void printMST( int parent[], int graph[][])
{
System.out.println( "Edge \tWeight" );
for ( int i = 1 ; i < V; i++)
System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);
}
void primMST( int graph[][])
{
int parent[] = new int [V];
int key[] = new int [V];
Boolean mstSet[] = new Boolean[V];
for ( int i = 0 ; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false ;
}
key[ 0 ] = 0 ;
parent[ 0 ] = - 1 ;
for ( int count = 0 ; count < V - 1 ; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true ;
for ( int v = 0 ; v < V; v++)
if (graph[u][v] != 0 && mstSet[v] == false && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
printMST(parent, graph);
}
public static void main(String[] args)
{
MST t = new MST();
int graph[][] = new int [][] { { 0 , 2 , 0 , 6 , 0 },
{ 2 , 0 , 3 , 8 , 5 },
{ 0 , 3 , 0 , 0 , 7 },
{ 6 , 8 , 0 , 0 , 9 },
{ 0 , 5 , 7 , 9 , 0 } };
t.primMST(graph);
}
}
Python
import sys
class Graph():
def __init__( self , vertices):
self .V = vertices
self .graph = [[ 0 for column in range (vertices)]
for row in range (vertices)]
def printMST( self , parent):
print "Edge \tWeight"
for i in range ( 1 , self .V):
print parent[i], "-" , i, "\t" , self .graph[i][ parent[i] ]
def minKey( self , key, mstSet):
min = sys.maxsize
for v in range ( self .V):
if key[v] < min and mstSet[v] = = False :
min = key[v]
min_index = v
return min_index
def primMST( self ):
key = [sys.maxsize] * self .V
parent = [ None ] * self .V
key[ 0 ] = 0
mstSet = [ False ] * self .V
parent[ 0 ] = - 1
for cout in range ( self .V):
u = self .minKey(key, mstSet)
mstSet[u] = True
for v in range ( self .V):
if self .graph[u][v] > 0 and mstSet[v] = = False and key[v] > self .graph[u][v]:
key[v] = self .graph[u][v]
parent[v] = u
self .printMST(parent)
g = Graph( 5 )
g.graph = [ [ 0 , 2 , 0 , 6 , 0 ],
[ 2 , 0 , 3 , 8 , 5 ],
[ 0 , 3 , 0 , 0 , 7 ],
[ 6 , 8 , 0 , 0 , 9 ],
[ 0 , 5 , 7 , 9 , 0 ]]
g.primMST();
C#
using System;
class MST {
static int V = 5;
static int minKey( int [] key, bool [] mstSet)
{
int min = int .MaxValue, min_index = -1;
for ( int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
static void printMST( int [] parent, int [, ] graph)
{
Console.WriteLine( "Edge \tWeight" );
for ( int i = 1; i < V; i++)
Console.WriteLine(parent[i] + " - " + i + "\t" + graph[i, parent[i]]);
}
static void primMST( int [, ] graph)
{
int [] parent = new int [V];
int [] key = new int [V];
bool [] mstSet = new bool [V];
for ( int i = 0; i < V; i++) {
key[i] = int .MaxValue;
mstSet[i] = false ;
}
key[0] = 0;
parent[0] = -1;
for ( int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true ;
for ( int v = 0; v < V; v++)
if (graph[u, v] != 0 && mstSet[v] == false
&& graph[u, v] < key[v]) {
parent[v] = u;
key[v] = graph[u, v];
}
}
printMST(parent, graph);
}
public static void Main()
{
int [, ] graph = new int [, ] { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
primMST(graph);
}
}
Javascript
<script>
let V = 5;
function minKey(key, mstSet)
{
let min = Number.MAX_VALUE, min_index;
for (let v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
function printMST(parent, graph)
{
document.write( "Edge Weight" + "<br>" );
for (let i = 1; i < V; i++)
document.write(parent[i] + " - " + i + " " + graph[i][parent[i]] + "<br>" );
}
function primMST(graph)
{
let parent = [];
let key = [];
let mstSet = [];
for (let i = 0; i < V; i++)
key[i] = Number.MAX_VALUE, mstSet[i] = false ;
key[0] = 0;
parent[0] = -1;
for (let count = 0; count < V - 1; count++)
{
let u = minKey(key, mstSet);
mstSet[u] = true ;
for (let v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
let graph = [ [ 0, 2, 0, 6, 0 ],
[ 2, 0, 3, 8, 5 ],
[ 0, 3, 0, 0, 7 ],
[ 6, 8, 0, 0, 9 ],
[ 0, 5, 7, 9, 0 ] ];
primMST(graph);
</script>
Output:
Edge Weight 0 - 1 2 1 - 2 3 0 - 3 6 1 - 4 5
Time Complexity of the above program is O(V^2). If the input graph is represented using adjacency list, then the time complexity of Prim's algorithm can be reduced to O(E log V) with the help of binary heap. Please see Prim's MST for Adjacency List Representation for more details.
?list=PLqM7alHXFySGHRB9iQ-jxdhLUriW-V6wr
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Finding Minimum Simple Spanning Tree With Solutions
Source: https://www.geeksforgeeks.org/prims-minimum-spanning-tree-mst-greedy-algo-5/